1. 状态空间表达式
Wk:过程噪声
Vk:观测噪声
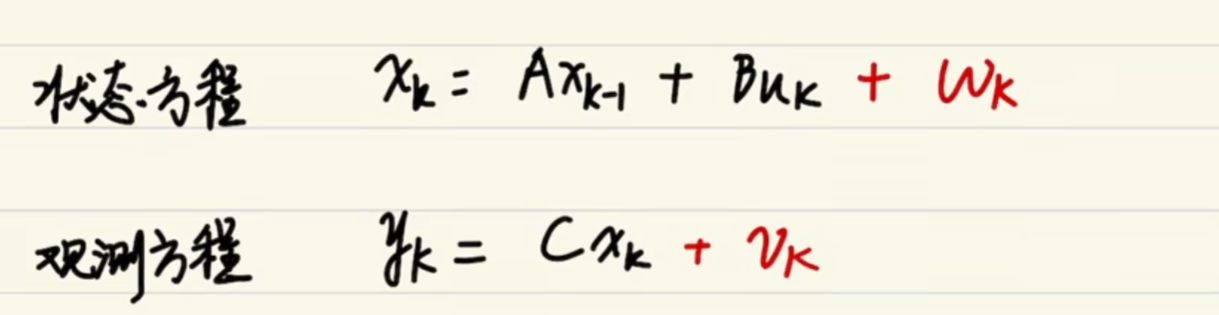
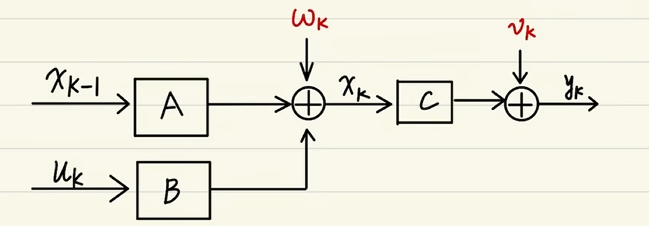
2. 系统框图
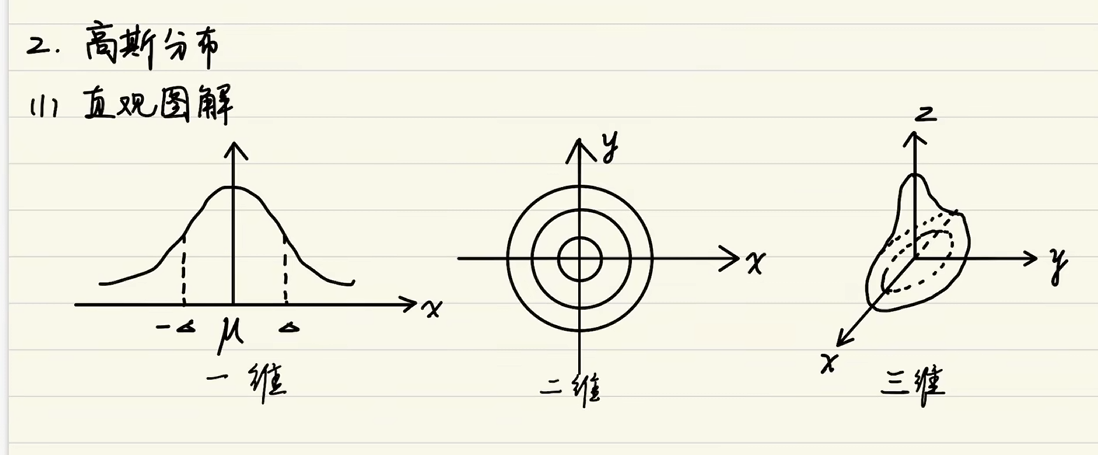
3. 高斯分布
卡尔曼滤波的噪声分布为高斯分布
 4
4

Wk,Q k的定义:
举个栗子:
一辆以大约5m/s行驶的小车,收到各种阻力的影响,运动速度为 V+Vr
实际速度为:5+ δ (m/s)
Wk = δ m/s
δ ∈ N(0;1)的高斯分布,Qk = 1
4. 协方差

Δ11就是cov(x1,x2)的简化形式

二维协方差
二维协方差(或称为协方差矩阵)是一个扩展了标准协方差概念的工具,适用于多维数据,特别是用于描述两个或更多变量之间的关系。在二维情况下,协方差矩阵可以用于表示两个随机变量 (X) 和 (Y) 的联合分布中的协方差。
协方差矩阵的表示
对于二维数据 ((X, Y)),协方差矩阵表示为:

其中:
- 是 (X) 的方差,表示 (X) 自身的波动程度。
- 是 (Y) 的方差,表示 (Y) 自身的波动程度。
- 是 (X) 和 (Y) 之间的协方差,表示它们之间的线性关系。
- 与 相等,因为协方差是对称的。
因此,二维协方差矩阵包含了两个变量的方差和它们之间的协方差。协方差矩阵的对角线元素是方差,非对角线元素是协方差。对于一个具有多个维度的变量,协方差矩阵扩展至更大的尺寸,以此方式描述多个变量之间的关系。
二维协方差矩阵的计算
假设有以下数据集 (X = [x_1, x_2, …, x_n]) 和 (Y = [y_1, y_2, …, y_n]),则二维协方差矩阵的计算可以按以下步骤进行:
计算每个变量的均值$ \overline{X}$ 和 。
计算每对变量之间的协方差,使用公式
构建协方差矩阵。
应用
二维协方差矩阵在以下领域有广泛应用:
- 多元统计分析
- 机器学习算法(如主成分分析)
- 金融分析
5. 超参数
卡尔曼滤波器主要调节两个参数:
:过程噪声的方差
R$:观测噪声的方差
卡尔曼滤波
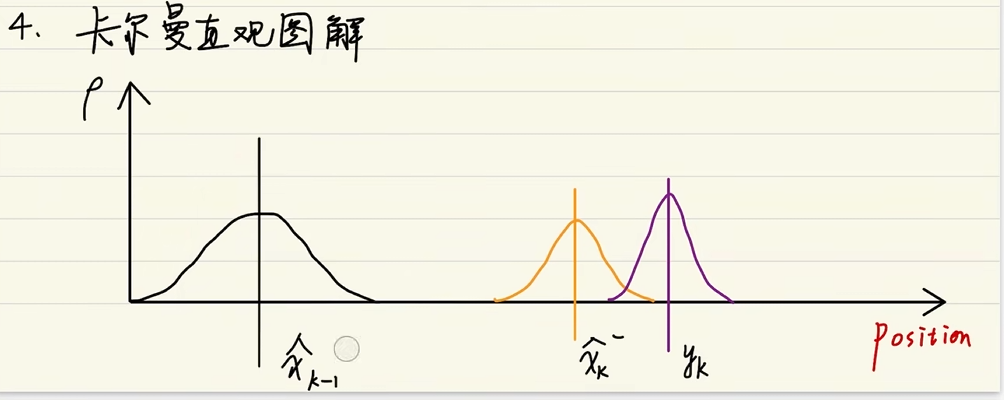
:最优估计值,后验,就是卡尔曼滤波器的输出值
:基于Xk-1的估计值,先验估计值
:传感器的测量值,当前时刻的观测值
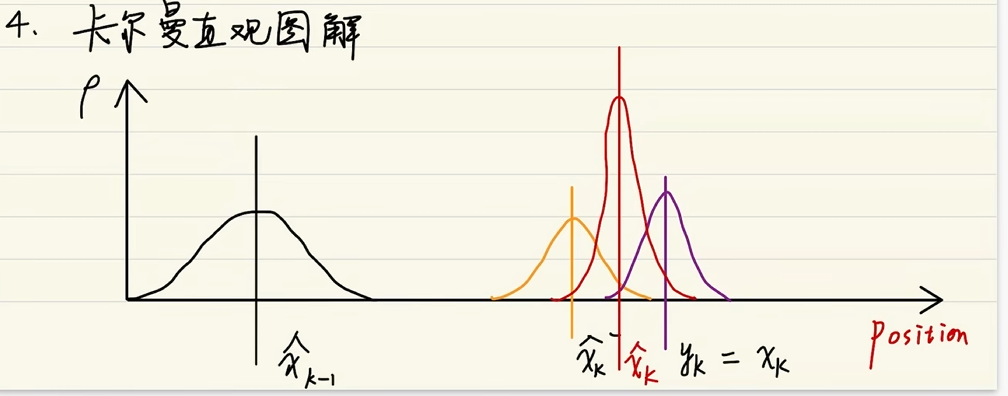
:当前的最优估计值
当前的最优估计值可以理解为先验估计值和测量值重合相关得到的结果。
卡尔曼滤波
一、实现过程
使用上一次的最优结果,预测当前的值,同时用观测值修正当前值,得到最优结果。
1 | # -*- coding: utf-8 -*- |
这段代码实现了一个一维匀加速运动中的卡尔曼滤波,用于估计物体的真实位置和速度。下面我们详细解释一下代码中每部分的含义,帮助你理解卡尔曼滤波的工作原理:
1. 问题背景
- 模拟的是一个匀加速直线运动的物体,其真实的运动受过程噪声(比如发动机噪声、风阻等)影响。
- 同时,测量设备(如 GPS 和 IMU)也会引入观测噪声,导致测量的位置和速度不够准确。
- 我们希望使用卡尔曼滤波方法,通过结合运动模型(预测值)和观测值,逐步估计物体的真实位置和速度。
2. 状态定义
状态包含两个变量:
-
位置
和
速度
:
-
3. 系统模型
-
状态转移模型 $$Xk+1=F⋅Xk+B⋅u+w$$:
-
:描述如何从当前的状态
XkX_kXk
预测下一时刻的状态。
- 假设一个单位时间 Δt=1\Delta t = 1Δt=1,位置通过公式 xk+1=xk+vk⋅Δtx_{k+1} = x_k + v_k \cdot \Delta txk+1=xk+vk⋅Δt 预测。
- 速度保持不变:vk+1=vkv_{k+1} = v_kvk+1=vk。
-
B=[1/21]B = \begin{bmatrix} 1/2 \ 1 \end{bmatrix}B=[1/21]
:控制矩阵,用于描述加速度对系统状态的影响。
- 加速度 uuu 对位置的影响是 12uΔt2\frac{1}{2}u\Delta t^221uΔt2,对速度是 uΔtu\Delta tuΔt。
-
www:过程噪声,用于模拟运动模型中的不确定性。
-
-
观测模型 Zk=H⋅Xk+vZ_k = H \cdot X_k + vZk=H⋅Xk+v:
- H=[1001]H = \begin{bmatrix} 1 & 0 \ 0 & 1 \end{bmatrix}H=[1001]:观测矩阵,表示测量设备直接观测位置和速度。
- vvv:观测噪声,模拟测量设备的误差。
4. 噪声和协方差矩阵
-
过程噪声协方差矩阵 QQQ
:描述运动模型中的不确定性。
- Q=[100010]Q = \begin{bmatrix} 10 & 0 \ 0 & 10 \end{bmatrix}Q=[100010]:这里假设位置和速度上的过程噪声是独立的。
-
观测噪声协方差矩阵 RRR
:描述测量设备的不准确性。
- R=[100000010000]R = \begin{bmatrix} 10000 & 0 \ 0 & 10000 \end{bmatrix}R=[100000010000]:这里假设位置和速度测量噪声也是独立的。
5. 卡尔曼滤波的步骤
卡尔曼滤波由两步组成:预测 和 更新。
(1) 预测步骤
-
状态预测:
Xk∣k−1=F⋅Xk−1∣k−1+B⋅uX_{k|k-1} = F \cdot X_{k-1|k-1} + B \cdot uXk∣k−1=F⋅Xk−1∣k−1+B⋅u
- 利用状态转移方程,预测当前位置和速度。
-
协方差预测:
Pk∣k−1=F⋅Pk−1∣k−1⋅FT+QP_{k|k-1} = F \cdot P_{k-1|k-1} \cdot F^T + QPk∣k−1=F⋅Pk−1∣k−1⋅FT+Q
- 协方差矩阵的预测,反映噪声和不确定性的传播。
(2) 更新步骤
-
卡尔曼增益:
Kk=Pk∣k−1⋅HT⋅(H⋅Pk∣k−1⋅HT+R)−1K_k = P_{k|k-1} \cdot H^T \cdot (H \cdot P_{k|k-1} \cdot H^T + R)^{-1}Kk=Pk∣k−1⋅HT⋅(H⋅Pk∣k−1⋅HT+R)−1
- 卡尔曼增益决定了如何平衡预测值和观测值的权重。
-
状态更新:
Xk∣k=Xk∣k−1+Kk⋅(Zk−H⋅Xk∣k−1)X_{k|k} = X_{k|k-1} + K_k \cdot (Z_k - H \cdot X_{k|k-1})Xk∣k=Xk∣k−1+Kk⋅(Zk−H⋅Xk∣k−1)
- 利用测量值 ZkZ_kZk,修正预测值。
-
协方差更新:
Pk∣k=(I−Kk⋅H)⋅Pk∣k−1P_{k|k} = (I - K_k \cdot H) \cdot P_{k|k-1}Pk∣k=(I−Kk⋅H)⋅Pk∣k−1
- 更新后的协方差矩阵,用于描述估计值的不确定性。
6. 代码的具体实现
- 生成真实值和观测值:
X_true:用运动模型生成真实位置和速度。Z:观测值通过添加观测噪声模拟。
- 卡尔曼滤波的预测和更新:
X_和P_:预测状态和协方差矩阵。K:计算卡尔曼增益。X和P:更新状态和协方差矩阵。
- 记录结果:
- 用
optim_positions和optim_speeds存储卡尔曼滤波的估计值。
- 用
7. 图示结果
- 位置图:
- 蓝色:真实位置(
real_positions)。 - 橙色:观测位置(
measure_positions,带噪声)。 - 绿色:卡尔曼滤波估计的最优位置(
optim_positions)。
- 蓝色:真实位置(
- 速度图:
- 蓝色:真实速度(
real_speeds)。 - 橙色:观测速度(
measure_speeds,带噪声)。 - 绿色:卡尔曼滤波估计的最优速度(
optim_speeds)。
- 蓝色:真实速度(
8. 关键理解
- 噪声影响:
- 观测值受噪声影响波动较大。
- 卡尔曼滤波通过结合模型预测和观测值,显著减小噪声的影响。
- 滤波过程:
- 早期估计可能与真实值偏差较大,但随着时间推移,滤波器逐渐收敛。
- 卡尔曼增益的作用:
- 决定了如何在观测值和预测值之间取权重,观测噪声越大,越依赖模型预测。
如果你对某一部分仍有疑问,可以详细提问,我会继续为你讲解!
您说:
为什么H是2x2的矩阵
ChatGPT 说:
ChatGPT
在卡尔曼滤波中,观测矩阵 HHH 的维度是由状态向量 XXX 和观测向量 ZZZ 决定的,其大小为 m×nm \times nm×n,其中:
- nnn 是状态向量的维度(这里是 2,因为状态 XXX 包括 [位置, 速度])。
- mmm 是观测向量的维度(这里是 2,因为观测值 ZZZ 包括 [位置, 速度])。
代码中定义的状态向量和观测向量为:
-
状态向量 XXX:
X=[xv]X = \begin{bmatrix} x \ v \end{bmatrix}X=[xv]
包含两个变量:位置 xxx 和速度 vvv。
-
观测向量 ZZZ:
Z=[zxzv]Z = \begin{bmatrix} z_x \ z_v \end{bmatrix}Z=[zxzv]
包含两个变量:测量的“位置” zxz_xzx 和测量的“速度” zvz_vzv。
因此,观测矩阵 HHH 是一个 2×22 \times 22×2 的矩阵,用于从状态 XXX 映射到观测 ZZZ。形式为:
Z=H⋅X+vZ = H \cdot X + vZ=H⋅X+v
为什么 HHH 是 2×22 \times 22×2 的单位矩阵?
在这个例子中,观测矩阵 HHH 被定义为:
H=[1001]H = \begin{bmatrix} 1 & 0 \ 0 & 1 \end{bmatrix}H=[1001]
这表示 观测值直接测量了状态中的位置和速度,且没有任何变换。具体来说:
-
第一行 [1,0][1, 0][1,0]:
- 表示观测值的第一个分量 zxz_xzx 对应状态中的位置 xxx,并且它与速度 vvv 无关。
zx=1⋅x+0⋅vz_x = 1 \cdot x + 0 \cdot vzx=1⋅x+0⋅v
-
第二行 [0,1][0, 1][0,1]:
- 表示观测值的第二个分量 zvz_vzv 对应状态中的速度 vvv,并且它与位置 xxx 无关。
zv=0⋅x+1⋅vz_v = 0 \cdot x + 1 \cdot vzv=0⋅x+1⋅v
这就说明测量设备可以分别直接得到位置和速度,且观测值和状态是一一对应的。
如果 HHH 不是单位矩阵怎么办?
在实际应用中,观测值可能与状态变量不是一一对应的,比如:
-
观测值只有位置(没有速度):
H=[10]H = \begin{bmatrix} 1 & 0 \end{bmatrix}H=[10]
这里,观测值只包含位置 xxx,不包含速度 vvv。
-
观测值是状态变量的某种线性组合:
H=[0.50.501]H = \begin{bmatrix} 0.5 & 0.5 \ 0 & 1 \end{bmatrix}H=[0.500.51]
这里,观测值的第一个分量是 0.5⋅x+0.5⋅v0.5 \cdot x + 0.5 \cdot v0.5⋅x+0.5⋅v,第二个分量是速度 vvv。
-
非线性观测: 如果观测值和状态的关系是非线性的,可能需要使用扩展卡尔曼滤波(EKF)或无迹卡尔曼滤波(UKF)来处理。
总结
在这个例子中,观测矩阵 HHH 是一个 2×22 \times 22×2 的单位矩阵,因为:
- 状态变量有 2 个(位置和速度),观测值也有 2 个(观测的位置和速度)。
- 观测值是状态变量的直接测量值,没有额外的变换或映射。
这种设计简化了问题,但在实际中可能会根据具体传感器和系统特性定义更复杂的 HHH 矩阵。
您说:
- 噪声和协方差矩阵 过程噪声协方差矩阵 𝑄 Q:描述运动模型中的不确定性。 𝑄 = [ 10 0 0 10 ] Q=[ 10 0 0 10 ]:这里假设位置和速度上的过程噪声是独立的。 观测噪声协方差矩阵 𝑅 R:描述测量设备的不准确性。 𝑅 = [ 10000 0 0 10000 ] R=[ 10000 0 0 10000 ]:这里假设位置和 为什么是10和10000
ChatGPT 说:
ChatGPT
在卡尔曼滤波中,过程噪声协方差矩阵 Q 和 观测噪声协方差矩阵 RRR 是滤波器的重要参数,它们用来描述系统模型和测量设备的不确定性。你提到的值 $$ Q=[100010]Q = \begin{bmatrix} 10 & 0 \ 0 & 10 \end{bmatrix}Q=[100010] 和 R=[100000010000]R = \begin{bmatrix} 10000 & 0 \ 0 & 10000 \end{bmatrix}R=[100000010000] $$是人为设定的超参数,代表对过程噪声和观测噪声强度的假设。这些值的选择取决于应用场景中的经验或者对系统的具体了解。
1. 为什么 QQQ 是 10
-
含义:QQQ 是过程噪声协方差矩阵,用于描述系统动态模型中的不确定性(即状态转移模型中可能的随机变化)。它反映了模型对自身预测的信任程度。
-
设置为 10 的含义:
-
在代码中,系统状态的两个变量是 [位置 xxx, 速度 vvv]。
-
设置
Q=[100010]Q = \begin{bmatrix} 10 & 0 \ 0 & 10 \end{bmatrix}Q=[100010]
表示:
- 每秒钟,位置和速度的预测值可能会受到方差为 10 的噪声影响。
- 换句话说,假设运动模型存在较小的不确定性,因为 10 是一个适中的值(与观测噪声相比)。
-
-
适用场景:这个值适合模拟一个较为简单、噪声较小的理想运动模型(例如匀加速运动),真实情况中可以根据实际系统的复杂程度调整。如果 QQQ 设得太小(接近 0),滤波器会过于相信模型而忽视观测值;如果设得太大,滤波器会对模型预测缺乏信任,可能过度依赖观测值。
2. 为什么 RRR 是 10000
-
含义:RRR 是观测噪声协方差矩阵,用于描述测量设备的不准确性(即传感器噪声)。它反映了测量值的可信度。
-
设置为 10000 的含义:
-
测量的两个变量是 [位置 xxx, 速度 vvv]。
-
设置
R=[100000010000]R = \begin{bmatrix} 10000 & 0 \ 0 & 10000 \end{bmatrix}R=[100000010000]
表示:
- 测量设备(比如 GPS 或 IMU)在每次测量时的噪声方差为 10000。
- 这意味着测量设备相对不精确,观测数据波动较大。
-
-
为什么观测噪声比过程噪声大很多:
- 通常,测量设备引入的噪声(例如 GPS 的位置误差、IMU 的速度误差)比运动模型的内在不确定性大得多。
- 在本例中,将观测噪声方差设为 10000,远大于过程噪声方差 10,表示测量数据不太可信,卡尔曼滤波器会更多地依赖运动模型预测,而不是直接相信观测值。
3. 参数选择的本质
-
过程噪声协方差 QQQ:
- QQQ 反映了对系统模型中随机性或不确定性的假设。
- 如果系统模型非常精确,且外部干扰较小(例如恒定加速度运动),可以设定较小的 QQQ。
- 如果系统模型存在较多不确定性(例如非理想运动),可以设定较大的 QQQ。
-
观测噪声协方差 RRR:
- RRR 反映了对测量设备精度的假设。
- 如果测量设备非常精确(例如高精度 GPS 或激光雷达),可以设定较小的 RRR。
- 如果测量设备不够精确(例如普通 GPS 或低质量 IMU),应该设定较大的 RRR。
-
两者的相对大小:
-
卡尔曼滤波器会根据
QQQ
和
RRR
的大小,动态调整对“模型预测值”和“测量值”的信任权重。
- 如果 Q≪RQ \ll RQ≪R(过程噪声远小于观测噪声):滤波器更相信运动模型的预测值。
- 如果 Q≫RQ \gg RQ≫R(过程噪声远大于观测噪声):滤波器更依赖观测值,而弱化对模型的信任。
-
4. 为什么选 10 和 10000?
这些值是经验性的超参数,可以根据实际情况调整:
- 10 作为过程噪声的方差,假设运动模型有一定的不确定性,但这种不确定性较小,符合匀加速直线运动的理想模型。
- 10000 作为观测噪声的方差,假设测量设备(例如 GPS 和 IMU)相对精度较低,观测数据波动较大。
5. 调整 QQQ 和 RRR 的影响
- 如果增加 QQQ:
- 过程噪声增大,滤波器会更不信任模型预测,更依赖测量值。
- 结果可能会更接近观测值,但波动性会增加。
- 如果增加 RRR:
- 观测噪声增大,滤波器会更不信任测量值,更依赖模型预测。
- 结果可能会更平滑,但与真实值的偏差可能会增加。
- 如果 QQQ 和 RRR 都变小:
- 滤波器对模型和测量的信任都会增加,可能更快收敛,但对噪声的鲁棒性会降低。
- 如果 QQQ 和 RRR 都变大:
- 滤波器对模型和测量都持较大怀疑态度,估计值可能会变得迟钝且收敛速度降低。
总结
- QQQ 和 RRR 的值是根据应用场景和对系统的了解设定的。
- 在这个例子中:
- Q=10Q = 10Q=10:假设运动模型的不确定性较小。
- R=10000R = 10000R=10000:假设测量设备的噪声较大。
- 这些值可以通过实验调整,以获得更好的滤波效果。如果你有真实数据,可以尝试调节这两个参数,观察滤波结果的变化!
您说:
X_true = F @ X_true + B * u + w的结果?
ChatGPT 说:
ChatGPT
在这段代码中,公式
Xtrue=F⋅Xtrue+B⋅u+wX_{\text{true}} = F \cdot X_{\text{true}} + B \cdot u + wXtrue=F⋅Xtrue+B⋅u+w
是用来模拟系统的真实状态更新的。下面我们具体分析其含义及结果。
1. 符号解释
-
Xtrue=[xv]X_{\text{true}} = \begin{bmatrix} x \ v \end{bmatrix}Xtrue=[xv]:表示系统的真实状态向量,包括位置 xxx 和速度 vvv。
-
F=[1101]F = \begin{bmatrix} 1 & 1 \ 0 & 1 \end{bmatrix}F=[1011]
:状态转移矩阵,用于描述理想的匀加速运动模型。
- 第一行:预测位置 xxx 时,考虑到上一时刻的位置 xkx_kxk 和速度 vkv_kvk 的影响(假设时间步长为 1)。
- 第二行:速度 vvv 在匀加速运动中保持不变。
-
B=[1/21]B = \begin{bmatrix} 1/2 \ 1 \end{bmatrix}B=[1/21]
:控制矩阵,描述加速度
uuu
对系统状态的影响。
- 对位置 xxx:加速度的影响是 12u⋅Δt2\frac{1}{2} u \cdot \Delta t^221u⋅Δt2。
- 对速度 vvv:加速度的影响是 u⋅Δtu \cdot \Delta tu⋅Δt。
-
uuu:加速度(设定为 0.6)。
-
www
:过程噪声(用随机数模拟的不确定性),表示真实运动状态的随机偏差。
- w=[wxwv]w = \begin{bmatrix} w_x \ w_v \end{bmatrix}w=[wxwv]:过程噪声对位置 xxx 和速度 vvv 的影响。
- wx∼N(0,Q[0,0])w_x \sim \mathcal{N}(0, Q[0, 0])wx∼N(0,Q[0,0]):位置噪声的标准差是 Q[0,0]\sqrt{Q[0, 0]}Q[0,0]。
- wv∼N(0,Q[1,1])w_v \sim \mathcal{N}(0, Q[1, 1])wv∼N(0,Q[1,1]):速度噪声的标准差是 Q[1,1]\sqrt{Q[1, 1]}Q[1,1]。
2. 更新过程
每一步的真实状态 XtrueX_{\text{true}}Xtrue 是通过以下公式计算的:
Xtrue=F⋅Xtrue+B⋅u+wX_{\text{true}} = F \cdot X_{\text{true}} + B \cdot u + wXtrue=F⋅Xtrue+B⋅u+w
逐项展开公式:
-
位置更新:
xtrue,new=xtrue+vtrue+12u+wxx_{\text{true,new}} = x_{\text{true}} + v_{\text{true}} + \frac{1}{2} u + w_xxtrue,new=xtrue+vtrue+21u+wx
- 原位置 xtruex_{\text{true}}xtrue。
- 加上速度 vtruev_{\text{true}}vtrue 的影响(假设时间步长为 1)。
- 加上加速度 对位置的影响。
- 加上噪声 。
-
速度更新:
- 原速度 。
- 加上加速度 对速度的影响。
- 加上噪声 。
3. 结果计算(示例)
假设当前的 ,即当前位置为 0,速度为 5;加速度 u=0.6u = 0.6u=0.6,过程噪声。设生成的噪声值为:
- (位置噪声)。
- (速度噪声)。
代入公式:
-
位置更新:
-
速度更新:
最终结果:
4. 真实状态的作用
在代码中,真实状态 是用来生成模拟的“测量值”(加入测量噪声后得到的观测值)以及作为对比卡尔曼滤波效果的参考。真实状态不可直接观测,但其模拟有助于理解卡尔曼滤波的性能。
5. 关键理解
- $F \cdot X_{\text{true}} $:根据理想模型更新状态。
- $ B⋅uB \cdot uB⋅u $:考虑加速度对系统状态的影响。
- :引入随机噪声,模拟现实中模型的不确定性。
最终的 $$X_{\text{true}}$$ 是理想模型、控制输入和随机过程噪声共同作用的结果。
您说:
卡尔曼滤波的英文
ChatGPT 说:
ChatGPT
卡尔曼滤波的英文是 Kalman Filter。
以下是与卡尔曼滤波相关的一些常见术语及其英文:
- 状态向量 (State Vector)
- 描述系统状态的变量(例如位置、速度等)。
- 状态转移矩阵 (State Transition Matrix)
- F (State Transition Matrix):描述系统状态从上一时刻到下一时刻如何演化的矩阵。
- 观测矩阵 (Observation Matrix)
- H (Observation Matrix):将状态映射到测量值的矩阵。
- 过程噪声 (Process Noise)
- w (Process Noise):描述系统模型中的随机不确定性。
- 观测噪声 (Measurement Noise)
- v (Measurement Noise):描述测量值中的随机误差。
- 过程噪声协方差矩阵 (Process Noise Covariance Matrix)
- Q (Process Noise Covariance Matrix):描述过程噪声的统计特性。
- 观测噪声协方差矩阵 (Measurement Noise Covariance Matrix)
- R (Measurement Noise Covariance Matrix):描述观测噪声的统计特性。
- 卡尔曼增益 (Kalman Gain)
- K (Kalman Gain):卡尔曼滤波中的权重,平衡预测值和观测值。
- 预测步骤 (Prediction Step)
- 在卡尔曼滤波中,用状态转移模型预测下一时刻的状态和协方差。
- 更新步骤 (Update Step)
- 利用观测值修正预测值,生成状态的最优估计。
卡尔曼滤波被广泛应用于控制系统、导航、信号处理和机器人等领域,用于融合预测模型和观测数据,降低噪声的影响,提供更准确的状态估计。
您说:
我要手动调节哪些参数
ChatGPT 说:
ChatGPT
在卡尔曼滤波中,手动调节参数是关键的一步,它直接影响滤波器的性能和估计效果。以下是需要手动调节的关键参数,以及它们的意义和调整建议:
1. 过程噪声协方差矩阵 ()
-
作用:描述系统模型中的不确定性,即状态变量(如位置和速度)随时间演变时引入的随机波动。
-
代码中的定义:
1
2Q = np.array([[10, 0],
[0, 10]])这里假设位置和速度的过程噪声是独立的,且方差均为 10。
-
调整方法:
-
增大
:
- 表示对系统模型的不确定性较高,滤波器会更依赖观测值。
- 滤波器会更敏感,估计值可能波动较大,但适合系统变化较快的情况。
-
减小
:
- 表示对系统模型较为信任,滤波器会更依赖预测值。
- 滤波器更平滑,但可能无法快速响应系统的快速变化。
-
-
建议:
- 如果系统的加速度、速度变化较大,设置一个较大的 。
- 如果系统比较稳定(如匀加速运动),则 可以设置较小。
2. 观测噪声协方差矩阵 ()
-
作用:描述测量设备的不确定性,即观测值中噪声的大小。
-
代码中的定义:
1
2R = np.array([[10000, 0],
[0, 10000]])这里假设测量噪声较大,位置和速度的测量误差独立,方差均为 10000。
-
调整方法:
-
增大
:
- 表示测量设备的精度较差,滤波器会更依赖系统模型的预测值。
- 滤波器估计值会更平滑,但可能与实际值偏差较大。
-
减小 RRR
:
- 表示测量设备的精度较高,滤波器会更依赖观测值。
- 滤波器估计值会更接近观测值,但波动会更大。
-
-
建议:
- 根据测量设备的精度选择合理的 值。
- 对精度较高的设备(如高精度 GPS),可以设置较小的 。
- 对噪声较大的设备(如低成本 IMU),应设置较大的 。
3. 初始状态协方差矩阵 ()
-
作用:描述对系统初始状态的不确定性。
-
代码中的定义:
1
2P = np.array([[0.1, 0],
[0, 0.1]])表示对初始位置和速度的置信度较高。
-
调整方法:
-
增大
:
- 表示对初始状态的不确定性较高,滤波器的收敛速度可能较慢。
-
减小
:
- 表示对初始状态较为自信,滤波器可能会更快收敛,但容易偏离真实值。
-
-
建议:
- 如果对初始状态了解不多,设置一个较大的 值。
- 如果对初始状态很自信(如已知初始位置和速度较准确),可以设置较小的 值。
4. 控制输入 () 和控制矩阵 ()
-
作用:控制输入描述系统受外力(如加速度)作用时的影响。控制矩阵 BBB 描述加速度对状态(位置和速度)的影响。
-
代码中的定义:
1
2
3u = 0.6
B = np.array([[1/2],
[1]])表示加速度, 描述加速度对位置和速度的影响。
-
调整方法:
- 如果系统中的加速度已知(例如匀加速运动),设置一个精确的 值。
- 如果加速度是未知的或不确定的,可以适当调整 或直接忽略控制输入。
-
建议:
- 如果没有加速度信息,直接将 设置为 0。
- 如果系统是匀加速运动,可以调整 以更好地拟合运动模型。
5. 时间步长 ()
-
作用:决定状态转移矩阵 FFF 和控制矩阵 BBB 中的数值,影响状态更新的精度。
-
代码中的默认值:假设时间步长为 1 秒。
1
2
3
4F = np.array([[1, 1],
[0, 1]])
B = np.array([[1/2],
[1]])- 如果时间步长为 ,状态转移矩阵和控制矩阵可以调整为: $$F = \begin{bmatrix} 1 & \Delta t \ 0 & 1 \end{bmatrix}, \quad B = \begin{bmatrix} \frac{\Delta t^2}{2} \ \Delta t \end{bmatrix}$$
-
调整方法:
- 如果采样频率较高(如每 0.1 秒采样一次),需要调整 FFF 和 BBB 的数值。
- 对较慢的系统(如每 10 秒采样一次),需要增加时间步长。
-
建议:
- 根据采样频率计算出准确的 Δt\Delta tΔt。
- 运动变化较快的系统使用较小的时间步长,较慢的系统可以适当增大。
6. 调节顺序和重点
调整卡尔曼滤波参数通常需要一些经验和实验,推荐以下顺序:
-
确定初始状态和协方差矩阵 ()
:
- 初始值影响滤波器的收敛速度。
-
调整观测噪声协方差矩阵 ()
:
- 根据传感器噪声水平调整 R$。
- RRR 越大,越相信模型预测值;越小,越相信测量值。
-
调整过程噪声协方差矩阵 ()
:
- 根据运动模型的复杂性和系统的不确定性调整 。
- QQQ 越大,越不相信模型预测值,滤波器对观测值更敏感。
-
调整控制输入 () 和时间步长 ()
:
- 根据系统的实际情况和外部控制输入调整。
总结
需要手动调节的关键参数:
- :过程噪声协方差矩阵,反映运动模型的不确定性。
- :观测噪声协方差矩阵,反映测量设备的不精确性。
- :初始状态协方差矩阵,反映对初始状态的不确定性。
- :加速度,描述外部控制输入的影响。
- $ \Delta t$:时间步长,影响状态转移矩阵和控制矩阵的设置。
通过实验调整这些参数,你可以优化卡尔曼滤波器的性能,使其更好地适应特定的应用场景。如果有真实数据,还可以通过优化算法自动寻找最优参数。
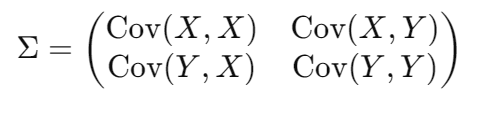

![【stm32单片机】[操作系统][RT-Thread][3]线程通信](/img/blog_cover/rt-thread.jpg)