一、独热编码
独热编码使用N位代表N种状态,任意时候只有其中一位有效。采用独热编码的例程:
独热编码使用N位代表N种状态,任意时候只有其中一位有效。
采用独热编码的例子
1 | 性别: |
独热编码的优点在于
- 能够处理非连续型数值特征
- 在一定程度上也扩充了特征。比如性别本身是一个特征,经过编码以后,就变成了男或女两个特征。
- 适合分类
在神经网络中,独热编码其实具有很强的容错性,比如神经网络的输出结果是 [0,0.1,0.2,0.7,0,0,0,0,0, 0]转成独热编码后,表示数字3。即值最大的地方变为1,其余均为0。[0,0.1,0.4,0.5,0,0,0,0,0, 0]也能表示数字3。
numpu中有一个函数,numpy.argmax()可以取得最大值的下标。
二、神经网络训练的重要概念
1. 输入(x)输出(y)、标签(label)
- 输入是指传入给网络处理的向量,相当于数学函数中的变量。
- 输出是指网络处理后返回的结果,相当于数据函数中的函数值。
- 标签是指我们期望网络返回的结果。
对于识别mnist图片而言,输入是大小为784(28 * 28)的向量,输出是大小为10的概率向量(概率最大的位置,即预测的数字),这部分操作由将长度为784的向量 xx 转换为长度为10的向量,是通过全连接层(Fully Connected Layer) 实现的。
2. 损失函数(loss function)
损失函数评估网络模型的好坏,值越大,表示模型越差,值越小,表示模型越好。因为传入大量的训练集训练的目标,就是将损失函数的值降到最小。
2.1 常见的损失函数定义:
差的平方和 sum((y - label)^2)
1 | [0, 0, 1] 与 [0.1, 0.3, 0.6]的差的平方和为 0.01 + 0.09 + 0.16 = 0.26 |
交叉熵 -sum(label * log(y))
1 | [0, 0, 1] 与 [0.1, 0.3, 0.6]的交叉熵为 -log(0.6) = 0.51 |
当label为0时,交叉熵为0,label为1时,交叉熵为-log(y),交叉熵只关注独热编码中有效位的损失。这样屏蔽了无效位值的变化(无效位的值的变化并不会影响最终结果),并且通过取对数放大了有效位的损失。当有效位的值趋近于0时,交叉熵趋近于正无穷大。
3. 回归模型
我们可以将网络理解为一个函数,回归模型,其实是希望对这个函数进行拟合。
比如定义模型为 Y = X * w + b,对应的损失即
1 | loss = (Y - labal)^2 |
可以通过不断地传入X和label的值,来修正w和b,使得最终得到的Y与label的loss最小。这个训练的过程,可以采用梯度下降的方法。通过梯度下降,找到最快的方向,调整w和b值,使得w * X + b的值越来越接近label。
机器学习-梯度下降算法原理及公式推导_梯度下降计算公式-CSDN博客
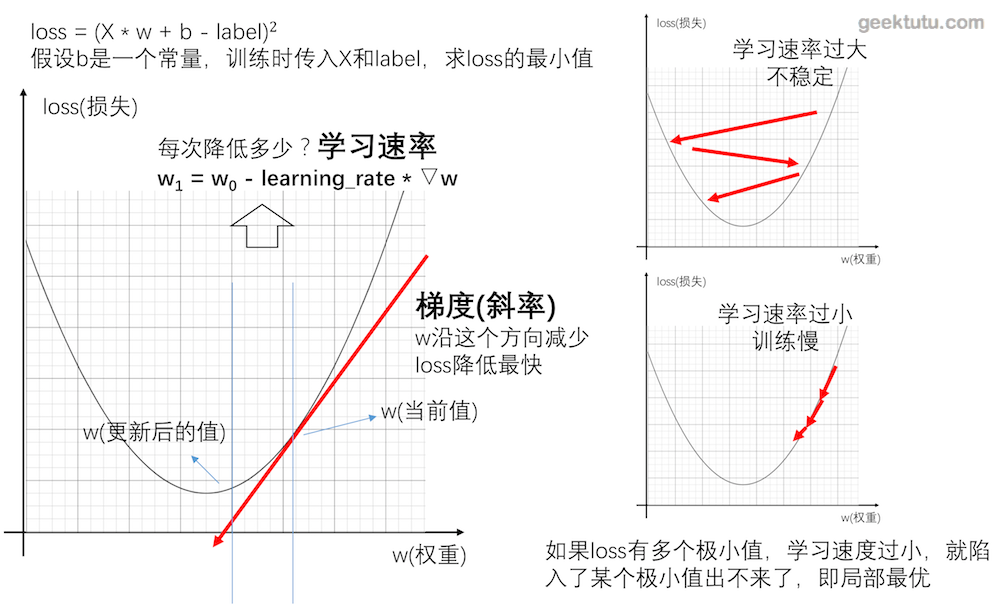
4. 学习速率
简单说,梯度即一个函数的斜率,找到函数的斜率,其实就知道了w和b的值往哪个方向调整,能够让函数值(loss)降低得最快。那么方向知道了,往这个方向调整多少呢?这个数,神经网络中称之为学习速率。学习速率调得太低,训练速度会很慢,学习速率调得过高,每次迭代波动会很大
5. softmax激活函数
作用:一是放大效果,二是梯度下降时需要一个可导的函数。
1 | def softmax(x): |
三、tensorflow识别手写数字-实现简单的神经网络
# 思考
一、输入x是 784长度的向量,什么机制使得输出y变成的长度为10的向量?
将长度为784的向量 xx 转换为长度为10的向量,是通过全连接层(Fully Connected Layer) 实现的。具体操作通过 权重矩阵 和 偏置向量 来完成。
1. 全连接层的基本机制:
全连接层的工作机制可以用矩阵乘法来描述。给定输入向量 xx(长度为784),要转换为长度为10的输出向量,通常通过如下步骤:
2. 步骤:
-
输入向量
:这是一个长度为784的向量,表示神经网络的输入。
-
权重矩阵
:全连接层会有一个权重矩阵 WW,其维度是 10×78410×784,表示从输入784维向量到输出10维向量的权重连接。每一行表示一个输出神经元与所有输入神经元的权重连接。
-
偏置向量
:偏置向量 bb 是一个长度为10的向量,表示每个输出神经元的偏置。
-
计算输出向量
:通过矩阵乘法计算输出向量。输出向量 oo 的维度是10。具体计算方式如下:
- W \cdot x ):矩阵 ( W ) 乘以向量 ( x ),将784维的输入向量映射为10维的输出向量。
-
假设输入向量
是长度为784的向量:
-
权重矩阵
是一个 10×78410×784 的矩阵:
-
偏置向量
是一个长度为10的向量:
-
输出向量
通过矩阵乘法和加法得到,维度为10:
每一行表示一个输出神经元的结果,最终得到一个长度为10的向量。
4. 激活函数:
在得到长度为10的向量后,通常会将其通过激活函数进行处理。在分类任务中,输出层通常使用 Softmax 函数,将每个输出值转换为概率值。Softmax 函数公式为:
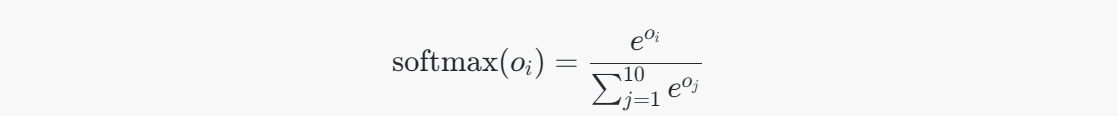
这会将输出向量 oo 转换为一个概率分布,表示输入属于不同类别的概率。
作用:对输出结果进行非负化和归一化,保证了概论的和为1
总结:
将784长度的输入向量变为10长度的输出向量的关键步骤是通过 全连接层的矩阵乘法 和 偏置项,最终计算出长度为10的向量,并通过 Softmax 函数将其转换为概率分布,从而实现分类。
二、Softmax
创建tensorflow训练代码
# 为什么图像要归一化处理?
在深度学习中,对图像数据进行归一化处理是一个重要的步骤,主要原因包括:
- 加速收敛:
- 当输入数据的范围相差很大时,神经网络的训练可能会变得非常慢。归一化可以使数据的分布更加一致,从而帮助优化算法更快地找到最优解。
- 提高模型性能:
- 不同的特征尺度会影响模型的学习效果。如果某些特征(如图像中的亮度)范围较大,模型可能会对这些特征过度敏感,导致其他特征的影响被抑制。归一化可以使得每个特征对模型的贡献更为均衡。
- 避免数值不稳定:
- 深度学习模型中的计算涉及大量的矩阵运算和梯度更新,未归一化的输入可能导致梯度消失或爆炸问题,这使得模型难以训练。通过归一化,可以减少这些问题的发生。
- 适应激活函数的输入范围:
- 一些激活函数(如Sigmoid和Tanh)对输入的值有特定的范围要求。归一化输入数据能够确保它们落在激活函数的有效区间内,从而提高模型的表达能力和训练效果。
常见的归一化方法
最小-最大归一化: 将数据缩放到或区间,公式为:

Z-score归一化: 通过均值和标准差对数据进行标准化,公式为:

其中,为均值,为标准差。
正则化到特定的均值和方差: 一些深度学习库(如TensorFlow和PyTorch)提供了方便的功能来对图像数据进行预处理,以保证其在输入到模型之前具有特定的均值和标准差。
在图像处理任务中,常见的做法是将像素值归一化到范围。这不仅能提高模型的训练效率,还有助于最终的预测性能。
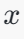 :这是一个长度为784的向量,表示神经网络的输入。
:这是一个长度为784的向量,表示神经网络的输入。
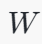 :全连接层会有一个权重矩阵 WW,其维度是 10×78410×784,表示从输入784维向量到输出10维向量的权重连接。每一行表示一个输出神经元与所有输入神经元的权重连接。
:全连接层会有一个权重矩阵 WW,其维度是 10×78410×784,表示从输入784维向量到输出10维向量的权重连接。每一行表示一个输出神经元与所有输入神经元的权重连接。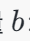 :偏置向量 bb 是一个长度为10的向量,表示每个输出神经元的偏置。
:偏置向量 bb 是一个长度为10的向量,表示每个输出神经元的偏置。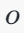 :通过矩阵乘法计算输出向量。输出向量 oo 的维度是10。具体计算方式如下:
:通过矩阵乘法计算输出向量。输出向量 oo 的维度是10。具体计算方式如下: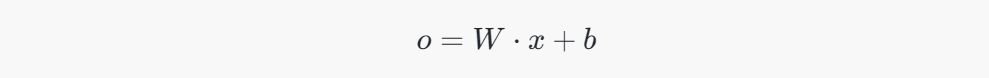




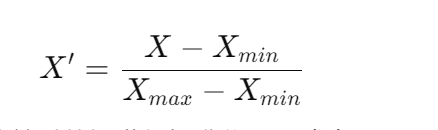
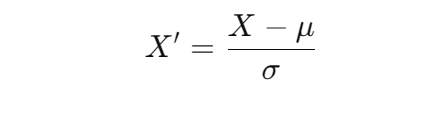

![【stm32单片机】[操作系统][RT-Thread][3]线程通信](/img/blog_cover/rt-thread.jpg)