一、PID的电机控制简易实现
pid模拟调参(无人机)
Webpack App (rossning92.github.io)
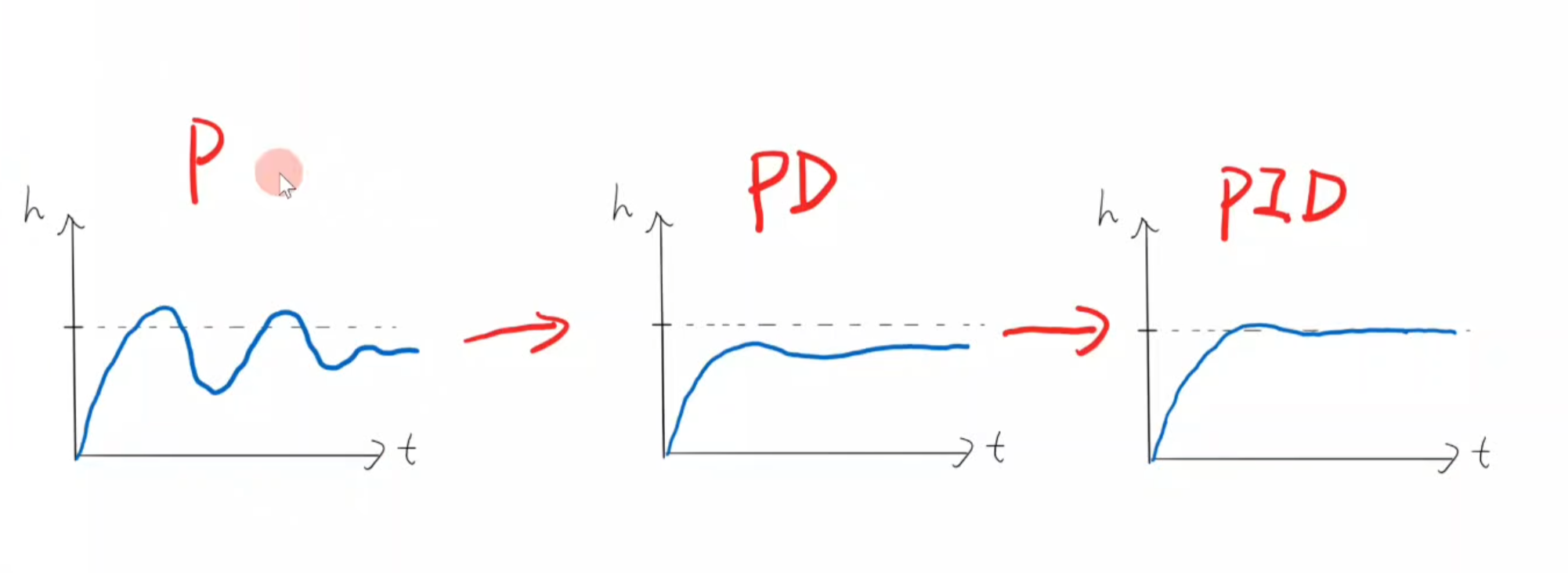
多环(平衡小车)

1 | int Kp,Ki,Kd; |
二、PID的基本原理

1. PID类型
增量式 PID 和位置式 PID 都是经典的 PID 控制算法,但它们在计算方式和控制策略上有所不同,适用于不同的控制场景。它们的主要区别如下:
1. 控制量计算方式不同:
- 位置式 PID:直接计算控制量的绝对值,也就是说,控制器输出的是相对于目标值的绝对控制量。控制输出值是当前误差的比例、积分、微分的总和。
- 增量式 PID:计算的是控制量的增量,也就是说,控制器输出的是相对于上一次输出的增量。每次输出的控制量是基于误差的变化量(增量)来进行调整的。
2. 计算公式的区别:
-
位置式 PID 公式:
u(t)=Kp⋅e(t)+Ki⋅∑e(t)+Kd⋅de(t)dtu(t)=K**p⋅e(t)+K**i⋅∑e(t)+K**d⋅dtd**e(t)
位置式 PID 直接根据误差
e(t)计算输出u(t),表示系统当前的绝对输出值。 -
增量式 PID 公式:
Δu(t)=Kp⋅[e(t)−e(t−1)]+Ki⋅e(t)+Kd⋅[e(t)−2e(t−1)+e(t−2)]Δu(t)=K**p⋅[e(t)−e(t−1)]+K**i⋅e(t)+K**d⋅[e(t)−2e(t−1)+e(t−2)]
增量式 PID 计算的是控制量的增量
\Delta u(t),然后将这个增量加到前一次的输出上。
3. 应用场景:
- 位置式 PID:适用于静态系统的控制,即系统状态稳定后,输出量应与设定值相匹配。例如,温度控制、液位控制等稳态控制系统。
- 增量式 PID:适用于动态系统,尤其是连续控制系统中,控制器仅需根据误差的变化调整控制量,不需要关心绝对控制输出值。例如,电机控制等场景,因为电机每次只需要根据偏差调整转速或位置,不关心当前的绝对输出值。
4. 累加与非累加:
- 位置式 PID:积分项是累加的,积分会不断积累误差,以便消除长期存在的偏差(消除稳态误差)。
- 增量式 PID:积分项不累加,积分是基于当前误差直接计算一个增量,只为下一个控制周期提供一个调整量。
5. 稳定性与抗干扰性:
- 位置式 PID:在长期误差较小时,由于积分项的累积,容易出现积分饱和问题,导致系统出现较大的超调。
- 增量式 PID:由于只计算增量,因此对外部干扰具有更好的抗干扰能力,并且不容易出现积分饱和的问题。
6. 控制器状态恢复能力:
- 位置式 PID:由于直接计算控制量的绝对值,如果系统意外断电,重新启动后需要重新计算出绝对控制量,恢复到正常状态可能需要更多时间。
- 增量式 PID:只根据增量调整,即使系统断电,重新启动后能够迅速恢复到正常状态,因为它只关心输出的增量变化。
7. 存储资源消耗:
- 位置式 PID:需要存储当前误差、积分累计值、微分计算的结果等。
- 增量式 PID:只需要存储上两次的误差值(
e(t-1)和e(t-2)),以及上一次的输出值,所需存储的资源较少。
总结:
- 位置式 PID:适用于系统状态稳定、要求精确控制的场景,输出的是绝对的控制值。容易产生积分饱和,适合稳态误差较小的系统。
- 增量式 PID:适用于动态控制场景,输出的是相对的增量变化,抗干扰能力较强,适用于快速响应和不关心绝对输出值的控制系统。
1.1 位置式PID
1.2 增量式PID
三、自整定PID
Enterprise_E/CODE/pid.c at main · ittuann/Enterprise_E (github.com)
1. Matlab快速参数整定的方法

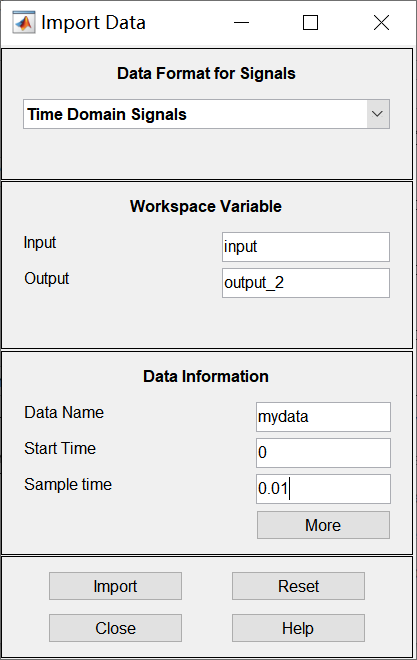
导入数据设置
- Input/Output:选择之前设置的输入输出数据
- 设置起始时间为0
- Sample time:采样时间,本图为10ms
PID和信号与系统(DSP)


本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Turin's Blog!

![【stm32单片机】[操作系统][RT-Thread][3]线程通信](/img/blog_cover/rt-thread.jpg)